







|
11A124
No Laffing Matter
by Jim Davies, 9/16/2011
Some weeks ago in Reality Check, I referred to the Laffer Curve; and thought today to give it a closer look - for it has something interesting to tell us. 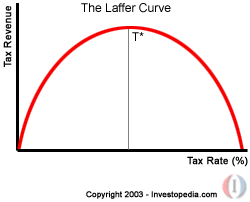
The Curve applies to individual incomes, aggregated to describe behavior in the whole society. Tax rates of 0% and 100% each produce zero tax revenue, but there must be a rate in between those extremes which produce a maximum grab for governments; usually the curve is drawn as a parabola with that peak at 50%, but the choice is arbitrary. The simple theory is that for everyone working and producing, there is some tax rate which disincents them to work; they prefer to devote effort to avoiding tax, or simply to enjoy leisure. This is not incorrect. However, suppose it's applied not to the aggregate of individual earnings, but to the nation's product in total; the Gross Domestic Product. The two seem at first to mean the same thing - but there's a key difference. GPD is defined to include the "product" of government activities, valued at what they cost. This is of course absurd, for if government pays a billion dollars a year to have ditches dug and filled in again, that billion counts towards GDP even though no rational person would choose to purchase that service. Therefore, since any rate of tax confiscates money from all contributors to GDP, government is taking money from itself with regard to its own component. It is not raising any new revenue there, but merely recirculating what it already has, at some non-zero cost. I assume here that it "taxes itself" at the same rate as it taxes everyone else, though that's an approximation; it's true about income taxes, and sometimes about property taxes (eg a city may tax federal property) but not about sales taxes. With that inaccuracy, for the true tax yield see the formula here. Let's suppose that 15% of government spending is useful, ie that it produces goods and services that people would buy anyway if offered in a free market. That part would yield genuine tax revenue if taxed. Suppose also that the cost of collecting taxes is 10%, from both the productive and the parasitic part of the economy. Then by that formula, net tax revenues are:
This shows 50% to 60% is an optimal rate from government's viewpoint. I then plugged in different values for the collection cost, between 5% and 25%, and it made little difference to that conclusion; but when I varied the estimate of how many of the government services are useful and marketable ("P") it did have a marked effect; the higher it was, the further to the right moved the optimal, max-tax rate:
So why don't governments impose taxes at rates higher than 60%? Because they know quite well that their delivered services are of low value and so that higher rates would yield lower revenues. Thus in most of Europe, where some government services are of relatively high quality, they get away with taxing people at 55% to 60% - suggesting that their services are perceived as being around 20% useful and marketable. Here in the US, the total tax rate is still about 50%, suggesting that we see their value as being 10% useful or less. Yes; that figures. Something fascinating follows: governments know it too, and by implementing tax rates that fit it well they admit that they know quite well that their "public" sector of the economy is indeed largely parasitic; ie, that its true market value is only around 10% to 20% of what it costs. Since they know that yet do nothing about it, we can accurately conclude from this alone that the purpose of power is power, not service. Long-time readers of this Blog will find no surprise there. But now, thanks to the Laffer Curve, that conclusion is backed by a little math.
|






|